The computational mechanics approach to Programmable Matter has been initiated in the Institute of Fundamental Technological Research of the Polish Academy of Sciences (IPPT PAN) in 2010, and then continued in collaboration with the University of Luxembourg and FEMTO-ST in France. The current line of research includes three main directions, which are planned to be eventually combined into a single mechanical framework for programmable matter.
Direction 1: Mechanical Tasks
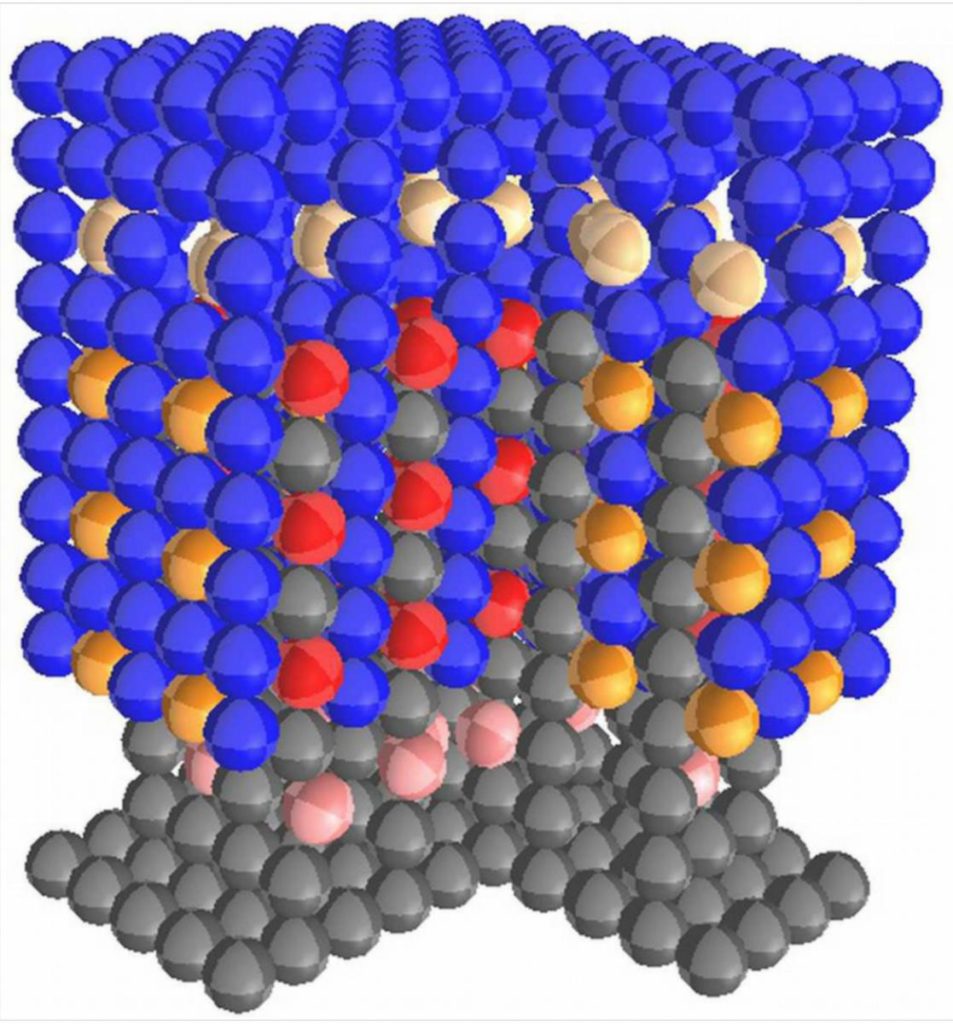
In real-world applications, Programmable Matter must be able to physically interact with the environment, perform mechanical tasks and be able to operate under load (e.g., the one generated by its own mass in the gravitational field). To this end, modular-robotic ensembles must be able to withstand and produce substantial forces. We propose, in particular, the concept of volumetric actuators – special modular-robotic structures which produce forces proportional to the ensembles’ size.
See more: [IROS 2014], [IROS 2015], [Robotica 2017]
Direction 2: Mechanically-aware reconfiguration planning
A self-reconfigurable robot is a mechanical system, which can break apart, fall over, collapse or damage an object it is interacting with. It is therefore desirable for the system to be aware of its current mechanical state (internal geometry, inter-modular connection loads or external constraints and forces) and to be able to predict what would be its state after a planned reconfiguration sequence. This constitutes a special mechanical problem to be solved by the distributed system itself and we work on algorithms for addressing it.
See more: [ICRA 2017], [IROS 2020], [IEEE T-RO 2021]
Direction 3: Efficient shape shifting
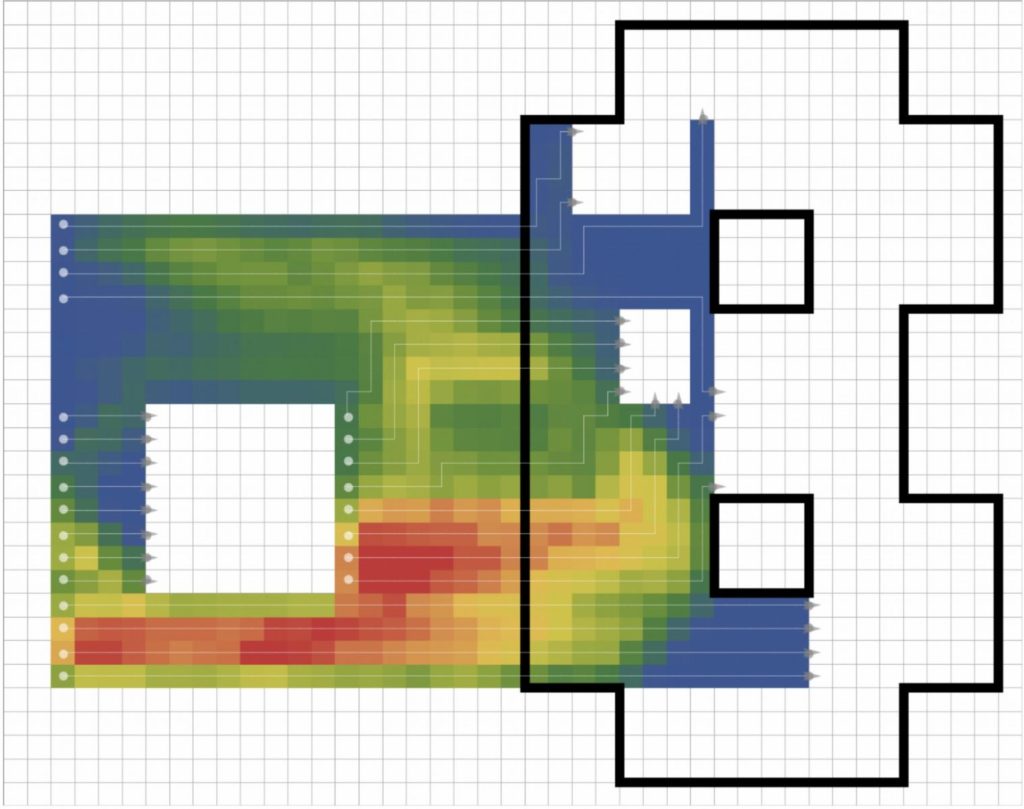
The usual approach to shape shifting only engages surface modules to move at one time, which is a limiting factor to parallelizing reconfiguration and can be extremely time-consuming for large ensembles. Following the idea of Stoy, we propose the paradigm of flow though a porous structure, which assures basic mechanical strength of the structure and allows a volumetric flow of modules. In our approach, we compute the optimal pathways to maximally parallelize the flow.
See more: [Autonom. Rob. 2019]